شب یلدای خود را چگونه گذراندید؟
پاسخ کوتاه: با محاسبهٔ اینکه «شب یلدا چهقدر طولانیتر است؟»
برای مشاهدهٔ این اثر هنری در کیفیت بالا، روی عکس کلیک کنید D:
پاسخ بلند: خب همونطور که حتماً میدونید، امشب شب یلدا بود. البته همچنان هم هست. طبقهٔ بالا پیش خانواده بودم و همینطور که اون ترانهٔ کذاییِ «آخ تو شب یلدای منی» توی ذهنم تکرار میشد، داشتیم از اهمیت و فضائل شب یلدا صحبت میکردیم و از این فلسفههای صدمنیهغازی که امشب طولانیترین شب ساله پس فلان کنیم و بیسار کنیم.
اینکه گفتیم طولانیترین شب سال، یهو بخش ریاضیدان ذهنم اومد جلو و پرسید حالا این طولانیترین شب که میگیم، چهقدر از شب قبلش طولانیتره؟ از مرتبهٔ ثانیه است یا ده ثانیه یا دقیقه؟ چطور میشه حسابش کرد یا تخمینش زد؟ همین رو از حضار پرسیدم. واکنش اول طبعاً این بود که بس کن بابا تو هم از هر داستانی یه مسئلهٔ ریاضی میکشی بیرون و حالا که به فرض فهمیدیم چهقدر طولانیتر، چه فایده؟! بخش سمج ذهنم به این حرفها قانع نبود و جواب میخواست. گفتم هرکسی یه حدسی بزنه. مامان گفت یه دقیقه یا سی ثانیه. به حساب اینکه توی ماه رمضون هر شب تا شب بعدش زمان اذان اینقدرا جابجا میشه. دامادمون حدس زد که دو سه ثانیه باشه. خودم هم همین حدود رو احتمال میدادم. یعنی زیر ده ثانیه. تحلیل من این بود که مدت روشنایی روز در طول یکسال باید یه حالت سینوسی داشته باشه. که کمترین و بیشترینش شب یلدا و روز یک تیر اتفاق میافته. اما میدونیم که مشتق تابع توی کمترین یا بیشترین مقدارش به صفر میل میکنه. یعنی تغییرات طول روز در شب یلدا، باید خیلی کمتر از تغییراتش در مثلا اول مهر باشه.
خب دست به قلم شدم تا ابعاد مسئله رو درک کنم. در نگاه اول، یک مسئلهٔ تخمین فیزیکی بود. از اینجور مسائل توی درس فیزیکیک داشتیم. سوال امتحان خودمون رو دقیق یادم نیست. ولی امتحانهای سالهای قبل، سوال داده بودند که چه انرژیای برای ساخت برج میلاد لازمه. یا مثلا چندتا خودرو توی محوطهٔ دانشگاهمون جا میشه. خب اینجا احتمالاً قراره یکسری ثوابت فیزیکی شعاع زمین و فاصلهٔ زمین تا خورشید و دورهٔ تناوب گردش زمین به دور خورشید و به دور خودش به کارمون بیاد. توی مسائل تخمین هم جواب دقیق مهم نیست. مرتبهٔ تخمین مهمه. یعنی از مرتبهٔ ده به توان چند؟ ده یا صد یا هزار یا ده هزار؟
یکم که دقیقتر شدم توی مسئله، متوجه شدم ریاضیاتش سختتر چیزی هست که انتظارش رو داشتم. اولین نکته این بود که یکسری زاویهبازی نیاز داره، ولی در فضای سهبعدی و نه دو بعدی. به سبک خانم میرزاخانی نشستم و با زاویهها بازی کردم ولی متاسفانه به سبک خانم میرزاخانی به نتایج تئوری مطلوبی نرسیدم! بذارید شما رو هم با زوایایی که توی این مسئله درگیر هستند آشنا کنم:
اولین و مهمترین زاویه، انحراف محوری زمین هست که با اپسیلون نشون میدیم و و حدوداً °۲۳ است. این عکس رو ببینید:
به ستارهٔ قطبی هم توجه کنید!
تمام ماجرای بهوجود اومدن فصلهای گرم و سرد و عید نوروز و شب یلدا و شب و روزهای طولانی قطب شمال و جنوب، برمیگرده به همین انحراف محور چرخش زمین دور خودش، با محور چرخشش دور خورشید. اگر چنین انحرافی وجود نمیداشت همیشه ۱۲ ساعت روز و ۱۲ ساعت شب بود. همیشه خورشید با زاویهٔ ثابتی میتابید و فصلها دیگه معنا نداشتند. ولی مثلا توی همین عکس بالا، داره تابستون رو در نیمکرهٔ شمالی نشون میده. خوشید با زاویهٔ بیشتری به نیمکرهٔ شمالی میتابه و هوا گرمتر میشه. ولی در نیمکرهٔ جنوبی که زمستونه، آفتاب اریب میتابه [و همچنین طول روز کوتاهتره]، پس هوا سردتر میشه. برای اهمیت زاویهٔ تابش، به این فکر کنید که یه برگهٔ کاغذ رو زیر بارون دست گرفتید. چه زمانی بیشتر خیس میشه؟ وقتی قطرات باران عمود باشند. ولی اگه به کاغذ زاویه بدید قطرات کمتری دریافت میکنه و شانس سالمموندنش بیشتره!
حالا چرا این انحراف محوری باعث کوتاه و بلند شدن طول روز میشه؟
سمت راست زمستون و سمت چپ تابستون رو نشون میده و ایران نزدیک خط بنفش بالاییه. همون طور که میبینید، در سمت راست وقتی زمین دور محورش بچرخه ایران مدت طولانیتری در تاریکی به سر میبره تا روشنایی. معکوس این اتفاق در تابستون میافته. زاویهٔ اپسیلون باعث میشه در تابستون مدت طولانیتری در روشنایی روز باشیم و شبهای کوتاهتری رو تجربه کنیم.
حالا زاویهٔ دوم وارد کار میشه: عرض جغرافیایی. توی تصویر بالا اگه حلقهٔ بنفشرنگ رو بالاتر یا پایینتر ببرید طول شب و روز تغییر میکنه. البته روی خط استوا همیشه طول روز ۱۲ ساعته. و اگه خیلی به قطب نزدیک بشیم، عملاً تمام روز تاریک یا روشنه. پس باید برای محاسبهٔ طول روز، عرض جغرافیایی منطقه رو بدونیم. من عرض جغرافیایی ایران رو °۳۰ در نظر گرفتم. (طول جغرافیایی اهمیتی نداره. مثلا ایران با کالیفرنیا حدود ۱۲ ساعت اختلاف زمانی (= ۱۸۰ درجه اختلاف فاز) داره ولی از نظر طول روز یا فصلها، شرایطمون یکسانه.)
زاویهٔ سوم، زاویهٔ زمین در چرخش دور خورشیده. یعنی اینکه توی کدوم نقطه از تصویر سیاهرنگ بالا قرار داره. اگه فرض کنیم سال ۳۶۰ روز هست. میتونیم با شروع از یک فروردین، هر یک روز رو معادل یک درجه حول این دایره بدونیم. پس شب یلدا معادل زاویهٔ ۲۷۰ درجه میشه. چرا سال رو ۳۶۵ روز نگرفتیم؟ چون در اون صورت محاسباتمون پیچیدهتر میشد. باید قوانین کپلر رو لحاظ میکردیم و مدار زمین رو بیضی و سرعت حرکتش رو متغییر میگرفتیم. فعلاً بیخیالش!
پس الان سهتا زاویه داریم. ε , φ , α. باید بر اساس این سه متغییر، تابعی برای محاسبهٔ طول روز برحسب ثانیه پیدا کنیم. اونوقت جواب نهایی مسئله برابر است با:
daytime(23°, 30°, 269°) - daytime(23°, 30°, 270°)
حالا اگر شکل مسئله رو بکشید، اگر اون زاویهٔ α اگر مضرب ۹۰ درجه نباشه، شکل سهبعدی میشه و خب درک کردن زوایا در فضای سهبعدی اصلا در تخصص من نیست!
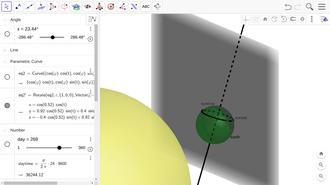
اینجا ریاضیاتم به در بسته خورد. ولی ذهن مهندسیام همچنان دنبال جوابی هرچند نادقیق بود. اومدم سراغ کامپیوتر. ابزار برنامهنویسی مناسبی برای حل اینجور مسائل ریاضی نداشتم. منظورم نرمافزارهایی مثل متلب و متمتیکا و.. است. دستبهدامان یه نرمافزار هندسی شدم. جئوجبرا. قبلا با بخش سهبعدیاش توی درس ریاضیدو کار کرده بودم. ابزار حرفهای به حساب نمیاد ولی برای کارهای آموزشی خوبه. توصیه میشه :).
خب اینجا یه کره رسم کردم در نقش زمین. یه دایره هم روی کره نیاز داریم که عرض جغرافیایی محل رو نشون بده. در واقع مسیری که کشور ما در طول یک شبانهروز طی میکنه. با تشکر از مختصات کروی! حالا باید انحراف محوری زمین رو پیاده کنیم. برای خود محور کاری نداره. میشه یه خط با شیب تانژانت زاویه. ولی برای خم دایره، باید در ماتریس دوران ضرب بشه. برای خورشید هم، با سینوس و کسینوس زاویه α محلش مشخص میشه و یه صفحه گذرنده از مرکز زمین میکشیم تا مشخص کنه چه بخشی روز و چه بخشی شب هست.
همون تصویر ابتدای پست، از زاویهٔ نیمرخ!
حالا کافیه دو نقطهٔ تقاطع خم دایرهای رو با صفحهٔ جداکنندهٔ روز و شب پیدا کنیم، که همون نقاط طلوع و غروب هستن. خوشبختانه تقاطع رو نرمافزار خودش پیدا میکنه. حالا با اندازهگیری فاصلهٔ دو نقطه و دونستن شعاع دایره، میتونیم زاویهٔ روز رو محاسبه کنیم. کل دایره ۳۶۰ درجه و ۲۴ ساعت (= ۸۶۴۰۰ ثانیه) است. پس با یک طرفینوسطین ساده، زمان روز برحسب ثانیه بدست میاد :).
پاسخ، این بار برای زاویهٔ ۲۶۹ (= روز ۲۹ آذر)
خب نهایتاً با یک عملیات تفریق، به جوابِ ۳۶۲۴۲٫۸۴ - ۳۶۲۴۴٫۱۲ میرسیم که برابر با ۱٫۲۸ ثانیه است. شب یلدا حدوداً یکثانیه از شب قبل و بعد از اون طولانیتره!
پانویس۱. همون طور که بالاتر اشاره کردم، من توی محاسبات سال رو ۳۶۰ روز گرفتم. در حالی که سال حدود ۳۶۵ روز هست. مسئلهای که اینجا مطرحه، اینه که طول ماهها دقیقا سیروز نیست. شش ماه اول سال هر کدوم یک روز بیشتر دارند. یعنی نیمهٔ اول سال حدود ۶ یا ۷ روز بیشتره. وقتی قوانینِ کپلر رو توی زمینشناسیِ دبیرستان رو خوندیم متوجه این موضوع شدم و یادمه کلی ذوق کردم با فهمیدنش! قانون اول و دوم کپلر بیان میکنن که مدار سیارات دور خورشید بیضی هست نه دایره، و خورشید در یکی از کانونهای بیضی قرار داره، و اینکه هرچه فاصلهٔ سیاره از خورشید بیشتر باشه سرعت حرکتش کاهش پیدا میکنه، به گونهای که مساحتی که در فواصل زمانی یکسان طی میشه برابره. کلید کار همینجاست: درسته که بهار و پاییز در دو نقطهٔ مقابل قرار دارند، ولی سرعت متفاوت گردش زمین باعث میشه طول بهار تا پاییز، طولانیتر از پاییز تا بهار باشه.
به هر صورت، من نتونستم به معادلهٔ مناسبی برای حرکت بیضی زمین دور خورشید برسم و با فرمولبندیهای قوانین کپلر هم مشکل داشتم. پس با فرض دایرهبودن مدار زمین پیش رفتم که البته خیلی هم بیراه نیست. نسبت قطر کوچک به قطر بزرگ مدار زمین حدوداً ۰٫۹۹۹۸۶ هست که خیلی نزدیک به یکه.
پانویس۲. خب اگه الان دارید با خودتون میگید چه آدم خُلوچِل و علافی، باید بگم که خودتون خُلید بابا. چطور میتونید از این حجم از زیبایی ریاضیات و قوانین طبیعت لذت نبرید؟ من به ازای هر یک از قضایایی که اینجا ذکرشون کردم، موقع فهمیدن اینکه چطور کار میکنند کلی ذوق کردم. مثلاً چطور میشه یه نفر داستان محاسبهٔ محیط زمین توسط اراتوستن رو بخونه و لذت نبره؟ یا همون داستان معروف ارشمیدس و اورکا اورکا گفتنش. خب باشه. شاید این شوق و ذوق داشتنم خیلی سطحی باشه و ارتباطی با کار واقعی دانشمندها نداشته باشه. ولی حتی اگه مثل ریچارد فاینمن دانشمند نشم، حداقل میتونم مثل پدر ریچارد فاینمن یک انسان عاشق دانش باشم. همین هم خیلی فوقالعاده است. اینطور نیست؟
پانویس۳. الان که دارم این پست رو منتشر میکنم ساعت ۴ صبحه. و امروز و فرداش دوتا کوییز دارم. اینو گفتم که اولاً اگه پست غلطملط املایی و نگارشی داشت ببخشید. ثانیاً برام دعا کنید که کوییزهام رو خوب بدم. ثالثاً ممکنه کامنتهای احتمالی پست رو دیر جواب بدم. [حالا خوبه هیچ کامنتی نگیرم و ضایع بشم D:]






1. خب اگه الان دارید با خودتون میگید چه آدم خُلوچِل و علافی، باید بگم که خودتون خُلید بابا.
این تیکه، بخش موردعلاقهی من از پست بودش! واقعا دیگه حرفی برای گفتن باقی نمیذاره، خییلی حال کردم باهاش :دیی
2. پستت یه جورایی خکم فیلمای نولان رو داشت برام از یه جهت، چطور؟ چون گاهی هرچقدرم که نفهمی داره چی میگه، بازم همینطوری دوست داری بری جلو و جلوتر تا ببینی به کجا میرسه نهایتا!
3. به دردم میخوره که بخوام وفت بذارم و برم جئوجبرا رو یاد بگیرم؟ واسه ریاضی2 ضروریه؟ میگم اگر لازمه، اینم بذارم تو برنامه و ذرهذره برم سمتش؟
4. شب یلدای هیجانانگیزی رو پشتِ سر گذاشتی! صمیما بهت تبریک میگم!
5. راستش دوست داشتم از نظر علمی حرف بیشتری برای گفتن داشته باشم، ولی خب باید اعتراف کنم که از فاز اول تفکراتت خیلی سر در نیاوردم، ولی بخشی که سپردیش به ذهن مهندسیت برام مفهومتر بود. فقط یه سوال برام پیش اومد. اگه ما یه واحدِ جدید برای اندازهگیریِ زویه تعریف کنیم، طوری که 2Pi rad، یا همون 360 درجه، بشه 365 واحد، و براساس این واحد جدیدمون مختصات و الباقی رو محاسبه کنیم، میتونیم یه جواب دقیقتر پیدا کنیم؟ یا مسئله خیلی پیچیدهتر از این حرفاست؟
+ منظورم اینه که مثلا به جای مقایسهی 269 و 270 از 360، بیایم 275 و 276 از 365 رو حساب کنیم؟ که خب با یه تناسب ساده، یعنی توی همین الگوریتمی که تو رفتی جلو، بیایم از 271.23 و 272.22 درجه استفاده کنیم؟
+ اصلا مطمئن نیستم منظور رو درست گرفته باشم و حرفایی که زدم معنایی دارن، یا خیر :دی
6. دعا هم نمودم :دی
7. مزیت بلاگ به تلگرام اینه که کاری به مجموعهها و اشتراک و استقلال و فلانشون نداره، مجموعهی مرجع زمان رو میگیره دستش، از اول شروع میکنه میآد جلو، هروقت شد، شد :دی